---

The Real Intelligence Training Academy (RITA)

---

Copyright 2025 by John H. Doolittle

---

A Gym to Develop the Skills Needed to Thrive in the World of AI

---

AI’s Weaknesses: What Does AI Need From You?

• AI is incapable of originality and true creativity. the engine is there, but someone need to steer.
• AI lacks judgement and tolerates wildly unworkable ideas.
• AI can’t handle novel situations

In other words, there is a serious need for flexible thinkers in this emerging world of AI.

---

Find Your Starting Point

---

Curious about your current problem-solving strengths? A great way to begin your R.I.T.A. journey is by taking a free self-assessment. This can help you understand your current cognitive profile and give you a baseline as you start training your mind.

Intelligence Self-Test Part 1:

Creative Reasoning

## DR. DOORIDDLE’S CREATIVE REASONING TEST FORM C (THE CRAZY RELATIVES)

©️2025 John H. Doolittle

### FORWARD

Kids are more creative than grownups. Why? Schooling. School relies on questions requiring convergent production: what does 2 + 2 equal? Students are required to provide a single, **CORRECT** answer. And, more importantly, **INCORRECT** answers are punished. “No, that’s WRONG.” This leaves little time for questions requiring divergent production: what would life be like if humans were born without opposable thumbs?

This is a test of **creative**, or **flexible**, thinking and requires **divergent production**. Consequently, there are no **CORRECT** answers. Some answers will be relatively better and more satisfying. The answers provided work pretty well but aren’t exclusive. If you truly like yours better, go with it.

—

### INSTRUCTIONS:

Examine each of the example puzzles below until you can see how each of the given words is related to its corresponding answer. You will have to be very flexible and imaginative. Look at each word from all sides, including similar words, like duck and goose; words that are opposites, like on and off; different words that sound the same, like air and heir, and words that can be combined, like pan and cake combine to make pancake. Turn your imagination loose and have some fun with it.

**NOTE:** Homophones are words that sound the same, but have different meanings and often different spellings.

For example: TO, TWO, TOO.

—

### SAMPLES with solutions:

* **CRIB CRY SIT = baby**

* **MOTOR LANE DIRT = bike**

* **DRIVE NAIL FINGER = thumb**

* **TRUCK NAIL FOOT = toe/ tow** (homophones)

* **POT PART SHOVEL = hole/whole** (homophones)

—

### TEST:

1. **NAIL INDEX PRINT =**

2. **PEPPER SPEAR GREEN =**

3. **MUG TEA BEANS =**

4. **HONEY SPELLING STING =**

5. **BASKET FOOT DANCE =**

6. **WITCH CASTLE BEACH =**

7. **CASE BED FIGHT =**

8. **TANK GOLD TAIL =**

9. **MELON BOTTLE WELL =**

10. **HAND TREE DATE =**

11. **INK PIG PLAY =**

12. **DEATH BOAT SENTENCE =**

13. **BUTTER HOUSE DRAGON =**

14. **CAP PAD JOINT =**

15. **ROOSTER BLACK SCARE =**

16. **POT PART SHOVEL =**

17. **ENGLISH FRY TOAST =**

18. **UNDER SLEEP DUE =**

19. **WALL SPARK DRAIN =**

20. **DOOR TRAFFIC STRAWBERRY =**

21. **MOON HOUSE BULB =**

22. **SANDWICH MARINE WAY =**

23. **STOCK SUPER FLEA =**

24. **CAMERA PLANT TROUBLE =**

25. **NUN CHIP KEY =**

—

### END OF TEST

---

Suggested answers in code: problem number, followed by number of letters of a popular answer, followed by first letter of same (Remember, if you honestly like your answer better, go with it!): 1. 6F, 2. 4M, 3. 6C, 4. 3B, 5. 4B, 6. 4S, 7. 6P, 8. 4F, 9. 5W, 10. 4P, 11. 3P, 12. 4L, 13. 3F, 14. 4K, 15. 4C, 16. 4H OR 5W, 17. 6F, 18. 4O, 19. 4P, 20. 3J OR 4J, 21. 5L, 22. 3S, 23. 6M, 24. 5S, 25. 4M.

Part 2: Deductve Reasoning Test

Who the Freg?

Six mod pods from outer space who had attempted to conceal their presence on earth by assuming common American names met recently over tea to discuss the pros and cons of investing in beach-front property. Among them were a Grig, an Ilk, a Freg, a Quarg, a Krig, and a Slok. Their American names were: Ash, Baker, Carr, Doyle, Emry, and Fink (not necessarily in the same order). From the following clues, tell who was who.

Emry and Doyle told the Slok, whom they hated, to take a class from Doolittle.

Either the Quarg was the Ilk or this is a hard puzzle.

Either Carr was the Grig or Baker was the Krig.

Baker and the Quarg beat Fink and the Grig at bridge.

Later, the Grig tried to eat the bridge.

Either Doyle was the Ilk or Baker was not the Slok.

The ilk was shorter than Emry but taller than Baker.

If Emry was the Krig, Baker was the Slok.

If we get one more puzzle, I’m going to kill somebody.

Ash was older than the Ilk who was older than the Grig by about 200 centons.

The Grig was shorter than Baker but taller than Doyle.

The answer is shown with all answers at the bottom of the site.

Part 3: Deductive Search Test

The following version of the Einstein 2% puzzle appeared in Life International in 1962:

1. There are five houses.
2. The Englishman lives in the red house.
3. The Spaniard owns the dog.
4. Coffee is drunk in the green house.
5. The Ukrainian drinks tea.
6. The green house is immediately to the right of the ivory house.
7. The Old Gold smoker owns snails.
8. Kools are smoked in the yellow house.
9. Milk is drunk in the middle house.
10. The Norwegian lives in the first house.
11. The man who smokes Chesterfields lives in the house next to the man with the fox.
12. Kools are smoked in the house next to the house where the horse is kept.
13. The Lucky Strike smoker drinks orange juice.
14. The Japanese smokes Parliaments.
15. The Norwegian lives next to the blue house.

Now, who drinks water? Who owns the zebra?

In the interest of clarity, it must be added that each of the five houses is painted a different color, and their inhabitants are of different national extractions, own different pets, drink different beverages and smoke different brands of American cigarets [sic]. One other thing: in statement 6, right means your right.

— Life International, December 17, 1962^[5]

For the answer and explanation, check the wikipedia page for Zebra Puzzle or Einstein 2% puzzle.

---

Introduction: Intelligence Isn’t Fixed. It’s Grown.

Welcome to the Real Intelligence Training Academy (RITA.), a step-by-step program designed to improve your problem-solving skills. This Academy operates on the core belief that your capacity for intelligence and problem-solving isn’t a static trait, but a skill you can strengthen and grow through dedicated practice.

---

WHAT IS INTELLIGENCE ANYWAY?

The Big Lie

“Intelligence is inherited and you are who you were born to be. It’s just the way things are.”

The Way Things Were

The world I grew up in had certain “truths” that seem foolish today:

• A Black man isn’t equipped to be President.
• A woman isn’t equipped to be a soldier.
• Joe isn’t endowed with the intelligence to succeed in college.

The claim was that people had natural, inborn traits that justified denying them opportunity. Many of these biases have wilted under the efforts of brave individuals who resisted them. George Miller, in his Presidential Address to the American Psychological Association, pointed out that throughout history, the revolutions that have led to lasting change have involved people changing their view of themselves. These are the people who have answered, “No, I can’t” with “Yes, I can!”

How Intelligence Was Defined

Unfortunately, the bias about the inborn nature of intelligence is still generally accepted. When I was a psychology graduate student, I was told, with a straight face, that “Intelligence can be defined as the trait that is measured by an intelligence test!” Are you kidding me? Look on the internet to see that the definition is still a mess. Here’s a quote from Wikipedia:

“Intelligence has been defined in many ways: the capacity for abstraction, logic, understanding, self-awareness, learning, emotional knowledge, reasoning, planning, creativity, critical thinking, and problem-solving. More generally, it can be described as the ability to perceive or infer information, and to retain it as knowledge to be applied towards adaptive behaviors within an environment or context.”

I think that’s called a kitchen sink definition: just throw in all the relevant words you can think of and hope that nobody notices that you don’t have a clue. Feel free to check Webster’s and other sources for equally clueless definitions.

The Capacity for Learning

Often you see the ability to learn mentioned as a key ingredient of intelligence. If so, say that and leave intelligence out of it. Of course, everyone is capable of learning a tremendous amount. To demonstrate, watch a toddler learn to speak his or her original language and think about what he or she is going through, and what you once went through. It is a monumental task of learning that we, somehow, accomplished. You were born into a world of meaningless sounds. You had to bring some kind of order out of the chaos. You had to sift through all the gibberish and learn to roll over, and stand up, and eat with a spoon! You had to discover the structure of language and gradually and painstakingly figure out how it all works. Watch a toddler and see how difficult and frustrating it is. But, does he or she give up? Did you? None of us did, partly because nobody was telling you that you couldn’t do it. Nothing you ever learned after that was as tough. College? Child’s play! You had proven your intelligence while still in diapers!

One Last Thing on Language: Nana

Picture the situation where the kid is first taught to say “Grandma,” a person you instantly warmed to as if you instinctively knew that this person was going to spoil you rotten and always take your side. By then, you knew that someone was trying to teach you the name for something and that your part of the game was to repeat that word back as best you could.

“Say, Grandma.”
“Na Na.”
“No, Grandma.”
“Na Na.”

At some point, Grandma intervenes, not for the last time, and says that you are perfect and never wrong and that she is fine with “Na Na,” which has much more charm than plain old Grandma. I point this out because it’s one of the few battles over how words are pronounced that the kids ever win. Na Na is never called Grandma again by anyone in the family.

---

Why Do We Do the Things We Do?

According to the pioneering psychoanalyst Alfred Adler and others, all human behavior is goal-oriented. We do what we do in order to achieve goals. Goals arise from basic needs, such as air, water, safety, and so forth, which you need to survive and thrive. Google Maslow’s ‘Pyramid of Needs’ for more information on human needs.

This is you: You breathe in or reach for a glass of water without really even thinking about it. “No Problemo,” as they say. This next example is a little more complicated:

Your goal, say, is to increase your attractiveness by getting a suntan while lounging on a tropical beach sipping a refreshing beverage.

As you proceed toward this goal, a barrier intervenes in the form of your boss, who calmly tells you that you may not have the time off. Problemo!

Let’s take another example and look closely at how a hunter deals with a major problem.

---

---

This hunter [figure 3], (based on the movie Never Cry Wolf), does not have a problem with respect to air: He breathes in and out without thinking about it. I’d like you to pretend that you are that hunter and are walking across a lake that has frozen over in winter.

Take a deep breath and move on to:

---

---

Because suddenly, you fall through the ice and sink to the bottom of the lake! Imagine how you would feel and what thoughts would run through your mind. You are probably not thinking, “What’s for lunch?” Unless I’m very mistaken, you sense that you will die here, and soon, if you can’t reach air. You imagine yourself swimming quickly to the surface and breathing. It’s like a movie in your mind, and you immediately start your desperate journey. Air sounds so good, like a cheeseburger to a backpacker.

---

But wait! Thanks to your big rifle and heavy backpack, you sank like a stone and will not easily swim to the surface with all that stuff. Even on the way down, you probably imagined a fantasy movie in which you are unable to do it. So, even before hitting the bottom, you probably begin lightening the load. Note how the main barrier to your goal generates preliminary barriers (problems) for you to solve.

*

Stepping back, we see that the process of problem-solving has twophases:

• Coming up with solutions to the problem.
• Trying them out.

The mental aspects of the two phases, let’s call creative thinking and critical thinking. More on this shortly.

For now, on to:

*

---

---

Alas, despite the fact you seem (to you) to have fallen straight down and swum straight up, there is no hole in the ice at the surface when you get there! Briefly, you may wonder where it went. Instead, there is a layer of ice. New preliminary problem! No worries, you’ll just punch a new hole and breathe. Just breathe.

Another alas. Your water-soaked parka arm strikes the ice feebly, and fails to break through. Panic time! Where’s that hole? Should you try to find it? Your next movie in your mind has you swimming to the hole and living. That movie is quickly followed by one with the less happy ending of swimming in the wrong direction.

So, sometimes, we test the solutions we’ve created by physically trying them out, as in the case of punching the ice. And, sometimes, we try them out and reject them entirely in our mind, as in gambling on which direction to swim.

---

The hunter doesn’t risk it. Instead, he analyzes the ineffective punch strategy and creates a solution using his more powerful legs. Yeah, baby.

On to

---

*

Alas, there are a lot of alases in problem-solving. Anyway: alas, the boot slides off of the ice ineffectually. The power is there, but the boot’s impact is spread too widely on the slippery underside of the ice.

Next plan: On to:

*

*

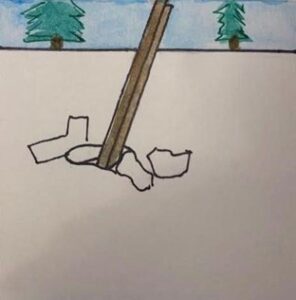
Thomas Edison (of light bulb fame) said, “I failed my way to success.” In other words, he used the results of numerous failed experiments to generate better and better hypotheses until success was achieved. The same goes for our hunter. He needs concentrated force, like an ice pick. Although the hunter’s sleeves are still sodden, he is able to point the rifle like a spear and thrust it upward into the ice. Luckily this metal barrel breaks through the ice with barrel to spare. With a couple of more thrusts, the hunter is able get his head out far enough to breathe!

The rest is easy.

*

---

 

 

Proof That Problem-Solving Training Improves Intelligence AND Creativity

I published a review of my research into improving thinking skills, including intelligence, in an article published in the American Psychological Association’s Journal Teaching of Psychology. To read the entire article, see: https://www.csus.edu/indiv/d/doolittle/papers.htm The section of research results is included here:

---

Here we go!

So, let’s get started making you a better problem-solver; or, more correctly, let’s get started on you making yourself a better problem-solver.

Although everyone is potentially a good problem-solver and life presents lots of problems, some people avoid the problem-solving process as much as they can and simply give up when life presents them with a difficult barrier. These persons change their goals or find someone else to remove the barrier for them. Frequently, these are both optimal solutions, but because problem solving lies at the core of living, even these avoidances tend to lower a person’s feelings of self-worth. On the other hand, improving one’s problem-solving ability does much to improve one’s feelings of self-worth. It seems that organisms, such as yourself, have something called competence motivation, which is a drive to have some control over the world they live in. Mice, for example, will learn a complex maze without any reward beyond just learning about their environment. It is probably this motive that is involved in the feelings of self-esteem that accompany increased competency in problem solving. You feel more in control of what is happening to you.

---

*

The Brain as a Muscle

It may be helpful in understanding your principle problem-solving organ, your brain, to think of it as a set of muscles. The muscle metaphor has a number of nice parallels. For example, overexertion is painful in both cases. Also, recovery from exertion becomes quicker after training.

Impossible Tasks

One form of resistance training for muscles is called isometrics and involves applying force to an immovable object. This process increases strength even though nothing seems to be happening. Similarly, when working on a problem that you are ultimately unable to solve, your brain is getting stronger because of the effort you are putting in, even though nothing seems to be happening. I hope this thought gives you some comfort, because some of the problems I will set before you in this book will be extremely difficult. If you try, there is no such thing as failure in this field of endeavor. You will improve if you just try!

---

*

How to Learn Problem-Solving Skills

*

Okay, if you go along with what has been said so far about problem solving, how does one learn these skills? What do we learn and what are the processes involved? Where do we start? One popular way to approach the acquisition of problem-solving skills is to make a list of all the processes anyone has ever used to solve a problem. These lists might include things like:

• recognizing that you have a problem,
• working backwards,
• making a list,
• drawing a picture,
• and so forth.

The various available lists run from about a dozen to about a hundred. Although others have had some success in teaching from these lists, I kept getting lost in the enormity of the task.

Let’s take the example of weight training? How would you go about acquiring competence in this area? One thing you might do is look for people who have already acquired the kind of competence you would like and ask them how they did it. Do they use machines or free weights?

Alternatively, you might approach a place that has an array of machines aimed at improving an array of muscle groups. Both of these approaches could be tried for problem solving as well. For the first, we could look at good problem solvers and see how their great achievements were accomplished. These great achievements might be building pyramids, landing a person on the moon, painting a great picture, or winning back-to-back Super Bowls. In some of these cases, the approach is well known and goes by the name of the scientific method. In the others, the approach is surprisingly similar, although not called the scientific method.

In the array of machines approach, one could attempt an array of problems aimed at strengthening an array of mental muscles. I once sat down to make a list of all of the kinds of problems that exist and found myself with a mercifully short list.

To begin with, I asked myself what are the characteristics of a problem and I answered that you could start at the end with the solution. For example, in the problem of where to find a copy of a book you would like to read, the solution (having and reading the book) is easily visualized. Sometimes, you have a problem, such as boredom, but don’t know which of several potential solutions is optimal. To solve any problem, you also need information about the problem (clues) which you can use to reach a solution. So now we have two components of problems: clues and solutions.

Now, what can we say about the clues we will need to solve a given problem? Well, for one thing, we either have all the clues we need to solve a problem or we have to seek additional clues to the ones we are given. The same can be said for potential solutions; i.e. they are either all available initially, or they have to be sought. In the finding the book problem above, the list of potential solutions (places where one could obtain the book) may be quite short; whereas, in the boredom problem, the list of potential solutions might take longer to think up than you have time to spend. In any case, we have now generated a two-by-two table of four types of problems, as shown below:\

---

A Two-by-Two Chart of All Problem Types

Any problem can be described by two components:

• Clues (information you need)
• Solutions (possible answers)

Each component can be available at the start or not yet available. Combine those options and you get four distinct categories of problems:

THE DOOLITTLE TYPOLOGY	Clues available initially	Clues not available initially
Solutions available initially	1 DEDUCTIVE REASONING	2 DEDUCTIVE SEARCH
Solutions not available initially	3 CREATIVE REASONING	4 CREATIVE SEARCH

*

The Doolittle Typology of Problems:

1. Clues and solutions all given – Deductive Reasoning. Simply apply logic to the clues (e.g., seeing the ocean tells you that you’re not driving toward Idaho).
2. Solutions given, clues missing – Deductive Search. Seek additional clues to test known solutions (e.g., toxicology screens to find poison in a victim’s coffee).
3. Clues given, solutions missing – Creative Reasoning. Generate solutions first, then evaluate them (e.g., re-imagining what “mask” means in a classic riddle).
4. Neither clues nor solutions given – Creative Search. Combine all skills; typical of big research efforts (e.g., inventing a cure for cancer requires new ideas and new data).

---

These four types will guide the exercises that follow:

DEDUCTIVE REASONING

Sometimes, deductive reasoning is called syllogistic reasoning or logical thinking. The word ‘syllogism’ refers to a form of reasoning consisting of two premises, which you assume to be true, and a conclusion which you can determine necessarily follows from or does not necessarily follow from the premises.

Disjunctive syllogism

This basic type of syllogism is sometimes called the process of elimination. It usually takes the form:

Premise #1: Either A is true or B is true.

Premise #2: A is false.

Conclusion: B is true.

To use a concrete example from everyday life:

Premise #1: Either I buy my kid a drone for his birthday or he’ll cry all day.

Premise #2: I don’t buy my kid a drone.

Conclusion: He’ll cry all day.

Do you think that the conclusion necessarily follows from the premises or not? In both cases above, it does.

Aside INSTRUCTION AND SELF-ESTEEM You may have noticed that the concrete second example is easier to follow than the abstract first example. Unfortunately, even having concrete examples is no guarantee that you to see the underlying rule. Sometimes, they only add to your confusion. I’ve found that students often too quickly take responsibility for their difficulty in understanding certain materials with words like “I’m just dumb in math” or “I can’t do logic”. Piffle and double piffle! As best I can tell from 40 years of teaching, just about anyone can learn just about anything. THE PRINCIPLE OF REACHABLE REACH The teaching principle needs to be what I call “Reachable Reach”. You want the problem solver to extend their problem-solving reach to its limit and still succeed. Failure can lead to discouragement. The trick is to start with what the individual student understands and build gradually upon that base. Luckily, if the problem-solver is pressed to their limit and succeeds, they not only feel good about themselves as problem-solvers (a basis for self-esteem), but they insulate themselves against failure and discouragement. After a number of these experiences, a cool thing happens: the problem-solver who tries something that doesn’t work, says to himself or herself, “Well, that didn’t work,” rather than “Well, I’ve failed.” THE SPECIAL CASE OF MATH INSTRUCTION The teaching of math in the public schools in America is a particularly egregious violation of the principle of reachable reach. In our regimented system, a lesson on carrying in arithmetic is followed with a lesson on borrowing, even if some students haven’t fully grasped the concept of carrying. The train moves inexorably along to more advanced concepts according to a schedule and students who fall off the train, often never get back on. That is a colossal shame. THE TALE OF THE NUN AND THE RULER I had a student once, who cried when I wrote a number on the chalkboard! I asked her about it and she said that she gets very emotional about math. She also said that she really wanted to major in Psychology and was afraid her lack of math skills would keep her from her dream. I asked her when this started and she recalled arithmetic flashcards that her nun/instructor held up in one hand. In her other hand was a ruler which was used to strike the slow or erring student across the wrist. I told her to stop me when she fell of the train and I went over the day’s lesson. She quickly stopped me and I was able to get her unstuck. She said, “That wasn’t hard!” I think the tutoring session took less than 15 minutes and didn’t need to be repeated. She worked hard and got an “A” in the class. She then went on to more advanced classes without difficulty. I later learned that she had received a Ph.D. in Psychology with an emphasis on statistical analysis!

Getting back to disjunctive syllogisms

An even more informal example of the process of elimination might be:

ME: “Darn! I lost my keys!”

HER: “Where might they be?”

ME: “Either in my pants or locked in the car.”

HER: “Are they in your pants?”

ME (sadly): “No.”

HER: “Then I suggest we go to the car. How are you with a coat hanger?”

HER does a great job here. First, she starts generating possibilities, namely, where are all the places your keys might be. Most poor problem solving involves a failure to consider enough possibilities. Second, she uses the process of elimination to direct attention to the car. Of course, ME may have been mistaken and they may find the keys on the ground on the way back to the car. Either way, they are well on their way to finding those darn keys.

Exclusive and non-exclusive ORs

In the keys example:

Premise #1: Either the keys are in the pants or the keys are in the car.

Premise #2: Keys not in the pants.

Conclusion: Keys are in the car.

What if they keys were in your pants? Could they be in the car? No, silly, they’re in your pants. This is an example of the exclusive OR, which means that one and only one part of the either … or … is true. In other words, if one part is true, the other part must be false.

Exclusive OR

Recall the birthday example:

Premise #1: Either I buy my kid a drone for his birthday or he’ll cry all day.

Premise #2: I don’t buy my kid a drone.

Conclusion: He’ll cry all day.

This is an example of a non-exclusive OR in that both parts of the either … or… can be true. That is, one part must be true and the other part can be true or not true. Thus, you could buy the drone and he could still cry all day! Although both parts can be true, they cannot both be false. One part, at least, must be true. You can usually tell which OR situation you find yourself in by the nature of the clues. For the puzzles and computer games you do in this guide, assume that every either… or… is an exclusive one unless you are explicitly told differently. Thus, if you find one part to be true, the other must be false, and vice versa.

Longer disjunctions

---

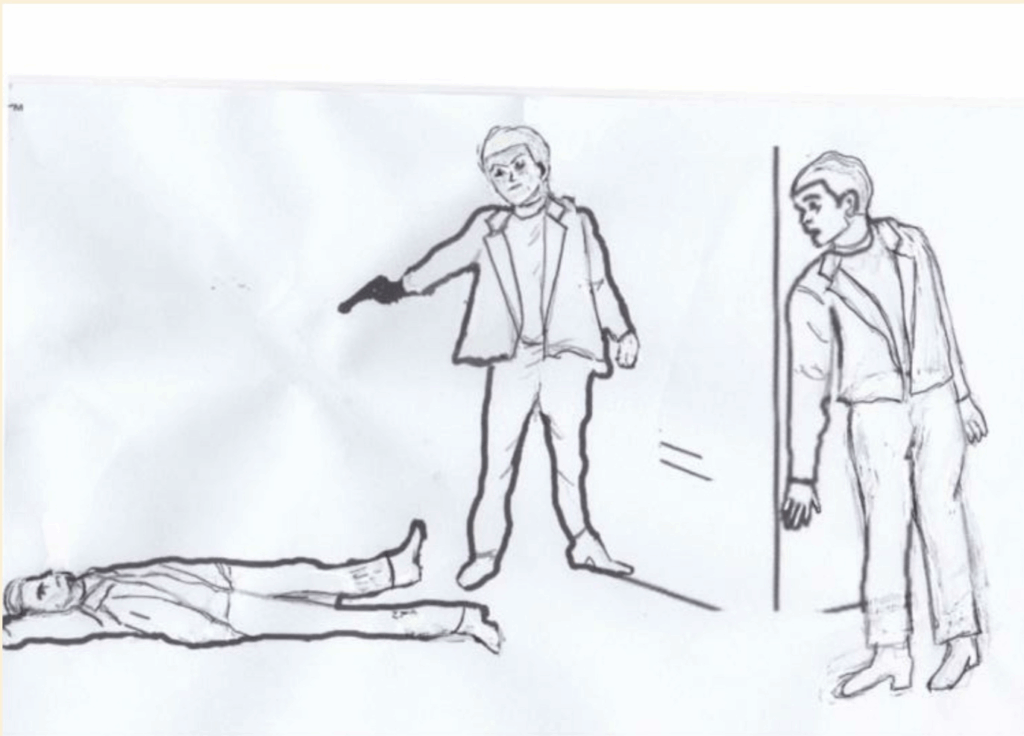
IN THE LIBRARY WITH THE REVOLVER

*

Let’s say that you are solving a mystery and you know that one of three characters Ash, Baker, or Carr, is the murderer. This is the equivalent of saying, “Either Ash was the murderer or Baker was the murderer or Carr was the murderer”. Let’s say, taking it a step further, that you learn that neither Baker nor Carr committed the crime. Then, you know, by the process of elimination, that Ash was the murderer. The disjunctive syllogism would look like this:

Premise #1: Either Ash was the murderer or Baker was the murderer or Carr was the murderer.

Premise #2: Baker was not the murderer and Carr was not the murderer.

Conclusion: Ash was the murderer.

Sure, no problem. Thus, we can have more than two parts to a disjunctive clue (premise #1) or to a conjunctive clue (premise #2) for that matter. A conjunctive clue says that this and that are both true.
Sometimes, deductive reasoning is called **syllogistic reasoning** or **logical thinking**. The word ‘syllogism’ refers to a form of reasoning consisting of two **premises**, which you assume to be true, and a **conclusion** which you can determine necessarily follows from or does not necessarily follow from the premises.

---

Matching puzzles


A popular form of deductive reasoning problem which uses longer disjunctive and conjunctive clues is the **matching puzzle**. These puzzles are often called **matrix puzzles** since they are often most easily solved using a matrix or chart. For example, take the murder with three suspects, Ash, Baker, and Carr, but this time one of them is the murderer, one is the witness, and one is the victim of the crime. Your task is to match the names of the characters with their role in the crime. To this end, you might find the following type of matrix useful in keeping track of the clues or information that you gather:

	MURDERER	WITNESS	VICTIM
ASH
BAKER
CARR

Now, if you find, say, that Ash was not the witness, you can put a “No” in the box where the Ash row intersects the Witness column and this can stand for the fact that Ash was not the witness. This is how it would look:

	MURDERER	WITNESS	VICTIM
ASH		NO
BAKER
CARR

Now, if you further find, say, that Baker was not the witness, you can add another “No” to the matrix:

	MURDERER	WITNESS	VICTIM
ASH		NO
BAKER		NO
CARR

Now, since somebody must have been the witness and you’ve eliminated Ash and Baker as suspects, Carr must have been the witness. You can put a “Yes” in the Carr-witness box:

	MURDERER	WITNESS	VICTIM
ASH		NO
BAKER		NO
CARR		YES

Now, if Carr was the witness (apologies to grammarians), Carr could not have been the murderer or the victim, and you can put “X” in each of those boxes:

	MURDERER	WITNESS	VICTIM
ASH		NO
BAKER		NO
CARR	X	YES	X

The reason I suggest using an “X” rather than a “No” is that each “No” in your matrix comes from clues that you are given, while each “X” follows from a “Yes”. This distinction is useful in recovering from a mistake should you ever make one. (Perish the thought!)

Now, suppose that other clues tell you that Ash was not the murderer. Then, you can put a “No” in the Ash-murderer box:

	MURDERER	WITNESS	VICTIM
ASH	NO	NO
BAKER		NO
CARR	X	YES	X

Since Ash was not the murderer and not the witness, Ash must have been the victim. Thus, you can put a “Yes” in the Ash-victim box:

	MURDERER	WITNESS	VICTIM
ASH	NO	NO	YES
BAKER		NO
CARR	X	YES	X

Now, if Ash was the victim, Baker could not have been the victim, and you can put an “X” in the Baker-victim box:

	MURDERER	WITNESS	VICTIM
ASH	NO	NO	YES
BAKER		NO	X
CARR	X	YES	X

Now, you only have one empty square which must hold a “Yes”. That is, Baker was the murderer, Carr was the witness, and Ash was the victim. Whew!

	MURDERER	WITNESS	VICTIM
ASH	NO	NO	YES
BAKER	YES	NO	X
CARR	X	YES	X

---

/

That was a lot, so, take a break and go over it again. The problems that you will solve in this guide will start out as three-name by three-role matrix puzzles. The paper-and-pencil puzzles below are up to six-name by six-role puzzles.

Types of Clues in Matching Puzzles

Affirmative Clues

The easiest clue you could get in a matching puzzle, such as the one above, would be an affirmative clue, such as “Ash was the murderer”. You could then put a “Yes” in and two “X”s in the matrix. If you were to buy a book of matching puzzles in a book or magazine store, they would mostly be very large puzzles with a lot of affirmative clues. To solve such a puzzle, you don’t need to know very many logical operators, but you do need to be careful marking a very large puzzle. Most of the errors that are made are clerical, rather than logical errors. Since I am more interested in teaching logical rather than clerical skills, we won’t be solving any very large puzzles.

Negative clues

Negative clues, such as “Ash was not the murderer”, lead directly to a “No” in your matrix and are really not much more difficult than affirmative clues. Of course, once you combine negatives with other elements, things get considerably more difficult. Say, for example, you learn that the statement, “Ash was not the murderer” is false. Concluding that “Ash must have been the murderer” is correct, but not easy.

Relational clues

These clues relate two or more characters or roles and are part of the linear syllogism. An example of a relational clue would be, “Ash is taller than the murderer”. Since you cannot be taller than yourself, Ash cannot be the murderer and you can put a “No” in the Ash–Murderer box.

Partial clues

A partial clue, such as “The murderer has blue eyes”, does not contain sufficient information, by itself, to put a mark on your matrix. Two or more partial clues must be combined to do that. For example, if one of the other clues was “Ash has green eyes”, then you could conclude that Ash was not the murderer, since Ash and the murderer have different colored eyes. In the world of puzzles, people have green eyes or blue eyes, while in the real world a person might have blue-green eyes. Some of the clues oversimplify complex situations. For example, the clues “Carr has blonde hair” and “The witness has brown hair” are presented so that you will correctly conclude that Carr was not the witness, even though we know blondness to involve the complex interplay of genetics and chemistry.

Conditional clues

These clues take the form “IF one thing is true THEN some other thing is true”. An example of this type of clue is “If Ash was the murderer THEN Baker was the witness”. Like the partial clues above, this clue must be combined with others to produce any conclusions. Take for example the following syllogism:

Premise #1: If Ash was the murderer then Baker was the witness.

Premise #2: Ash was the murderer.

Conclusion: Baker was the witness.

This is a valid syllogism and the conclusion is correct. These clues can make a puzzle quite difficult. In Premise #1, the statement after the IF (“Ash was the murderer”) is called the antecedent and the statement after the THEN (“Baker was the witness”) is called the consequent. Both the antecedent and the consequent can be shown to be true (affirmed) or false (denied). The syllogism above is an example of affirming the antecedent, a valid form of syllogism.

Denying the antecedent

Denying the antecedent is an invalid or fallacious form of syllogism. For example:

Premise #1: If Ash was the murderer then Baker was the witness.

Premise #2: Ash was not the murderer.

Conclusion: Baker was not the witness.

This conclusion does not necessarily follow from the premises. If you found the rule hard to see because this example is not very clear, you are not alone. The choice of a good, clear example is the most important part of teaching these rules. My favorite example comes from Anita Harnadek and involves the easy-to-visualize elements of rain and clouds. Here is the denying the antecedent fallacy in weather terms:

Premise #1: If it is raining then there must be clouds in the sky.

Premise #2: It is not raining.

Conclusion: There are no clouds in the sky.

This is much easier to diagnose as fallacious because you can readily visualize a counter-example; namely a cloudy day without rain. One of the drawbacks to the advent of television (as compared with books and radio programs) is the general decline in visualization and imagination. People get so used to having the pictures made for them, that they lose the ability to visualize imaginative pictures in their mind. Unfortunately, the central component of problem solving is the creation and manipulation of mental models (pictures) of a universe. The computer simulation adventure games that will be recommended later are all in text so that you will be forced to visualize a ghost town or a pirate’s island. Fortunately, visualization is a learnable skill and you will improve as you work on it. Hopefully, you will be nearly as imaginative when you complete these exercises as you were at age six. Imagination is not generally rewarded in our schools and gradually falls out of the average person’s repertoire. No one is unimaginative by nature, only by conditioning over time.

Affirming the consequent

With affirming and denying both the antecedent and the consequent, you have four possibilities, of which we have considered two so far: affirming the antecedent (valid) and denying the antecedent (invalid). The next is affirming the consequent (invalid):

Premise #1: If Ash was the murderer then Baker had blue eyes.

Premise #2: Baker had blue eyes.

Conclusion: Ash was the murderer.

This, again, is pretty tough as stated. Let’s translate it into rain and clouds:

Premise #1: If it is raining then there must be clouds in the sky.

Premise #2: There are clouds in the sky.

Conclusion: It is raining.

Nonsense, just because there are clouds in the sky, doesn’t mean that it is raining. We can all visualize a cloudy day without rain that shows this form of syllogism to be invalid. What I recommend with a tough syllogism like the one above about blue eyes is to recopy the syllogism on paper and write the word rain above the antecedent and clouds above the consequent in the conditional premise and the corresponding term above the other premise. I promise that this will help heaps.

Denying the consequent

Since we have considered three syllogism forms and two have been invalid, you would probably guess that the fourth was valid and it is. Denying the consequent is the most difficult of the four forms. For example:

Premise #1: If Ash was the murderer then Baker was the witness.

Premise #2: Baker was not the witness.

Conclusion: Ash was not the murderer.

Perfectly valid, but kind of hard to see. Now, with rain and clouds:

Premise #1: If it is raining then there must be clouds in the sky.

Premise #2: There are no clouds in the sky.

Conclusion: It is not raining.

All you have to do is visualize a cloudless, sunny day and you will have no trouble concluding that it cannot be raining without some clouds. Be careful with this one.

Distractors

All that we have left to consider is distractors. Distractors are clues that the author throws in to throw you off. Distractors take on of three forms:

• redundant
• clearly irrelevant
• seemingly relevant

Redundant clues confirm something that you already know to be true and serve to slow you down. Of course, if you have reasoned incorrectly, a redundant clue can help to get you back on the right track.

Clearly irrelevant clues are only there to slow you down and break your concentration. For example, in a murder puzzle you may see the clue, “The victim regrets the whole thing.” Don’t try to make too much of that sort of clue!

Finally, we have seemingly relevant distractors that lead to one of the fallacies listed above. For example, “Ash had blue eyes and the murderer had blue eyes”. Would you conclude that Ash was the murderer? Better not. Ash and/or Baker might have had blue eyes also. This distractor invites an affirming the consequent fallacy. You could restate the clue that the murderer had blue eyes (with respect to Ash) as follows:

Premise #1: If Ash was the murderer then Ash had blue eyes.

Premise #2: Ash had blue eyes.

Conclusion: Ash was the murderer.

Try this with rain and clouds to make certain that you see the counter-example that shows this form of reasoning to be fallacious. Nearly all fallacies involve an inability to think of a counter-example when one exists. For this reason, I feel that training in imagination development is the best training for fallacy detection (more on this later).

Sample Puzzles

Let’s start with these:

In the following, Ash, Baker, and Carr are murderer, witness, and victim in no particular order. Doyle, Emry, and Fink are innocent bystanders. Each puzzle is a fresh crime. Draw a matrix in the space provided.

Puzzle 1

1. Carr has red hair.
2. Baker was taller than the Witness.
3. The Murderer has brown hair.
4. The Murderer was shorter than the Witness.

Who’s who?

Puzzle 2

1. Either Ash was not the Murderer or Carr was older than Doyle.
2. Baker has a degree in Physics.
3. Doyle is older than Ash.
4. The Murderer never took any science classes in college.
5. Ash is older than Carr.
6. The Witness and Baker played Emry and Fink in tennis.

Who’s who?

Puzzle 3

1. Ash was meaner than Doyle.
2. Carr and Doyle beat Emry and the Witness at pickle ball.
3. The victim was not as mean as Doyle, but meaner than Carr.

Who’s who?

Puzzle 4

1. Either Baker was older than Doyle or Carr was not the murderer.
2. Carr and Emry were better at tennis doubles than Fink and the victim.
3. Doyle was the oldest.
4. If Carr wasn’t the murderer, Baker wasn’t the victim.

Who’s who?

Puzzle 5

1. If Carr was the victim, Baker was taller than Emry.
2. Either Carr was the victim or Ash was not the witness.
3. Emry was the tallest.
4. Ash was older than the victim.

Who’s who?

OR THESE:

A:

1. CARR WAS TALLER THAN DOYLE

2. ALL MEMBERS OF THE BUZZ CLUB HATED BEES

3. BAKER WAS MORE INTELLIGENT THAN DOYLE

4. BAKER WAS A MEMBER OF THE BUZZ CLUB

5. THE WITNESS WAS SHORTER THAN DOYLE

6. ASH THOUGHT THAT I.Q. WAS A MARTIAL ART

7. DOYLE WAS TALLER THAN BAKER

8. THE MURDERER WAS LESS INTELLIGENT THAN DOYLE

9. THE WITNESS LOVED ALL INSECTS

#1: ASH=____________ BAKER= ______________CARR= _______________

B:

1. THE WITNESS NEEDED TO PUT ON A FEW POUNDS

2. ASH ALWAYS HAD MINTY-FRESH BREATH

3. BAKER WAS STRONGER THAN EMRY

4. BAKER ONCE KILLED A FLY BY BREATHING ON IT

5. THE VICTIM WAS WEAKER THAN DOYLE

6. ASH WAS OVERWEIGHT

7. CARR LIKED THOSE LEAN FROZEN DINNERS

8. THE VICTIM’S LAST BREATH WAS ALSO BAD

9. EMRY WAS STRONGER THAN DOYLE

#2: ASH=__________ BAKER= ______________CARR= ____________

C:

1. CARR HAD BLUE EYES

2. THE MURDERER WAS BALD

3. THE VICTIM LIKED EGGPLANT

4. ASH HAD GREEN EYES

5. NO MEMBER OF THE SAC SOCIETY LIKES EGGPLANT

6. BAKER HAD LESS HAIR THAN DOYLE

7. THE MURDERER HAD GREEN EYES

8. ASH STILL HAD A FULL HEAD OF HAIR

9. CARR WAS A MEMBER OF THE SAC SOCIETY

#3: ASH=____________ BAKER= ______________CARR= __________

D:

1. BAKER WAS LIGHTER THAN DOYLE

2. EMRY WAS TALLER THAN DOYLE

3. FINK LIVED ON OAK STREET

4. ASH AND EMRY WERE ON A DIET

5. EMRY AND DOYLE WERE FIRST COUSINS

6. ASH LIVED NEXT DOOR TO FINK

7. EITHER ASH WAS NOT THE VICTIM OR DOYLE WAS TALLER THAN FINK

8. I DON’T THINK THIS WAS COVERED IN THE BOOK.

9. IF ASH LIVED ON OAK STREET THEN ASH WAS NOT THE WITNESS

10. EMRY WAS SHORTER THAN FINK

11. THE VICTIM WAS HEAVIER THAN DOYLE

#1: ASH=____________ BAKER= ______________CARR= _______________

E:

1. DOYLE LIVED AROUND THE CORNER FROM EMRY

2. FINK WAS PLANNING A TRIP TO TAHITI

3. IF DOYLE WERE THE UGLIEST THEN EMRY COULDN’T SWIM

4. EITHER DOYLE WAS A CATHOLIC OR THE COWS WILL NOT COME HOME

5. IF ASH WERE THE MURDERER THEN DOYLE LIVED ON ELM STREET

6. F CARR WERE THE MURDERER THEN DOYLE WAS THE UGLIEST

7. EMRY HATED THE TROPICS

8. EMRY LIVED ON ELM ST

9. EITHER 5 + 2 = 8 OR EMRY SWIMS WELL

10. EITHER CARR WAS NOT THE VICTIM OR DOYLE WAS NOT A CATHOLIC

11. THE COWS WILL COME HOME

#2: ASH=____________ BAKER= ______________CARR= _______________

F:

1. IF BAKER WERE THE MURDERER THEN EMRY LIKED SUSHI

2. ASH WAS MEANER THAN DOYLE

3. BAKER COULD NOT SWIM

4. CARR WAS MEANER THAN BAKER

5. IF DOYLE LIKED SUSHI THEN BAKER WAS NOT THE MURDERER

6. THE WITNESS OWNED A RED SWIMMING SUIT

7. THE WITNESS WAS THE MEANEST

8. BOTH DOYLE AND EMRY LOATHED SUSHI

9. CARR OWNED NOTHING THAT WAS RED IN COLOR

#3: ASH=____________ BAKER= ______________CARR= _______________

---

Rules for the games that follow:

1. Fill the matrices with YESs, NOs, and Xs.
2. Recopy all IF…THEN… syllogisms below the matrix and write the words, RAIN and CLOUDS in the appropriate places.
3. Recopy all EITHER…OR… syllogisms below the matrix and write the words TRUE and FALSE in the appropriate places.
4. For all NOs, include the clue line numbers in the upper right corner of the cell.

---

Who the Freg?

Six mod pods from outer space who had attempted to conceal their presence on earth by assuming common American names met recently over tea to discuss the pros and cons of investing in beach-front property. Among them were a Grig, an Ilk, a Freg, a Quarg, a Krig, and a Slok. Their American names were: Ash, Baker, Carr, Doyle, Emry, and Fink (not necessarily in the same order). From the following clues, tell who was who.

1. Either the Quarg was the Ilk or this is a hard puzzle.
2. Either Carr was the Grig or Baker was the Krig.
3. Baker and the Quarg beat Fink and the Grig at bridge.
4. Later, the Grig tried to eat the bridge.
5. Either Doyle was the Ilk or Baker was not the Slok.
6. The ilk was shorter than Emry but taller than Baker.
7. If Emry was the Krig, Baker was the Slok.
8. If we get one more puzzle, I’m going to kill somebody.
9. Ash was older than the Ilk who was older than the Grig by about 200 centons.
10. The Grig was shorter than Baker but taller than Doyle.
11. Emry and Doyle told the Slok, whom they hated, to take a class from Doolittle.

	Grig	Ilk	Freg	Quarg	Krig	Slok
Ash
Baker
Carr
Doyle
Emry
Fink

Answer

Ash =		Baker =		Carr =
Doyle =		Emry =		Fink =

---

The rock stars

Recently, the leaders of six major rock groups (The Acid Punkins, The Deadly Nightshades, The Castored Whatnots, The Librium Expression, The Functional Dichotomies, and The Web of Deceit) whose names (not necessarily respectively) were Ash, Baker, Carr, Doyle, Emry and Fink, met recently to discuss the rumor that AI had written the last four #1 songs.

1. The Dichotomy, who was into computers, believed the rumor, but Emry and Fink did not.
2. The Whatnot used more glitter than Fink.
3. Baker was the least loaded.
4. Emry was more into fusion than The Expression, but less into it than The Whatnot.
5. If Carr was not a Web, he was not a Whatnot.
6. If Ash was a Web, Doyle was not an Expression.
7. Either Doyle was the Expression or Fink was not the Punkin.
8. If Emry was a Web, Carr was a Web.
9. Doyle was less into fusion than Emry, who was less into it than Fink.
10. Either Emry was a Web or Fink was not a Web.
11. Carr was not as loaded as the Web, but more loaded than Doyle

	Acid Punkin	Deadly Nightshades	Castored Whatnots	Librium Expression	Functional Dichotomies	Web of Deceit
Ash
Baker
Carr
Doyle
Emry
Fink

Answer

                              Ash =                                    Baker =                                      Carr = 

                          Doyle =            Emry =              Fink =  

Deductive search strategies

In a sense, all problem solving is the search for a solution to a problem. The term, deductive search strategies, however, is usually restricted to problems where all of the solutions, but not all of the clues are present initially. The subcategories are:

■           random search

■           split-half search

■           systematic trial and error search

Random search refers to any of a variety of inefficient, haphazard search techniques that don’t need to be taught.

Split-half search  refers to the attempt to divide the problem space, or domain of possible solutions in half. For example, in the game of 20 Questions, if I learned that the object was a geographical location on earth, I might ask if it is in the northern hemisphere. A “yes” would eliminate the lower half of the globe and a “no” the upper half. By the way, the game of 20 Questions is an all-around excellent game for creative solution generation as well as searching and I recommend it to you most highly.

Systematic trial and error search uses indirect proof or the method of contradiction or the process of elimination (many names for the same thing) to eliminate all of the impossible possibilities until one possibility, the answer, remains (if you remember your Sherlock Holmes). In the game, Queue, the process of elimination involves the systematic keeping of records of guesses and conclusions, and on the application of the denying the consequent syllogism:

Premise #1: If it is raining then there must be clouds in the sky.

Premise #2: There are no clouds in the sky.

Conclusion: It is not raining.

In the game Queue3, there are three Londoners waiting in a queue (line) for a bus. Their names are: Ash, Baker, and Carr and we are concerned with the order in which they find themselves in line on this particular day. The possible orders are:

First	Second	Third
Ash	Baker	Carr
Ash	Carr	Baker
Baker	Ash	Carr
Baker	Carr	Ash
Carr	Ash	Baker
Carr	Baker	Ash

For convenience, let us shorten these to ABC, ACB, BAC, BCA, CAB, and CBA. Let’s go through a game of Queue3 to get a feel for how the game is played.

To begin with, you are given no information about the order of the queue and must make a guess to get things started. Suppose we guess Ash first, Baker second, and Carr last in the queue. To enter our guess, we type ABC and press the enter key. If that was the correct order, the computer would say, “Well done!” and return with a fresh puzzle for you to solve. If that was not the correct order, the computer would tell you how many of the three chaps (Ash, Baker, and Carr) you had in the correct spot in the QUEUE. Suppose that the computer responded to our guess, ABC, with the information that we only had one of the chaps in the right order, what could we conclude? For starters, we now know that ABC is not the correct order because the computer or phone didn’t say, “Well done!”

Looking at this conclusion syllogistically, we have the following denying the consequent syllogism: Premise #1: If ABC were the correct order then the computer would have said “Well done!” Premise #2: The computer did not say “Well done!” Conclusion: ABC was not the correct order.

If you are not absolutely comfortable with this syllogism, write the words “rain” and “clouds” in the appropriate place until you are comfortable. Using this syllogism, we can eliminate other possible orders based on the information in the clue. Let us consider each of the other five possible orders in turn. (Did I warn you that this is a tedious game? Sorry, please bear with me.)

Premise #1: If ACB were the correct order then the computer would have said one chap in the correct order. (Ash is the only chap in the same place in the queue in ABC [our guess] and ACB [the potential answer].)

Premise #2: The computer did say one chap is in the correct order. Conclusion: No conclusion possible.

To conclude anything would be an affirming the consequent fallacy. If you recall:

Premise #1: If it is raining then there must be clouds in the sky.

Premise #2: There are clouds in the sky. Conclusion: It is raining.

 We cannot be certain that ACB is the correct order and we cannot be certain that it is not. 

On to the next, BAC:

Premise #1: If BAC were the correct order then the computer would have said one chap in the correct order (as ABC and BAC have Carr in the same spot).

Premise #2: The computer did say one chap is in the correct order. Conclusion: No conclusion possible.

Same reasoning as ACB. 

On to BCA:

Premise #1: If BCA were the correct order then the computer would have said no chaps in the correct order (as ABC and BCA have no chaps in the same spot in the queue).

Premise #2: The computer did not say no chaps are in the correct order (recall that it said one chap).

Conclusion: BCA cannot be the correct order.

Recall the following:

Premise #1: If it is raining then there must be clouds in the sky.

Premise #2: There are no clouds in the sky.

Conclusion: It is not raining.

So, BCA cannot be the correct order.  This syllogism, denying the consequent or modus tollens in fancy logic talk is hands down, the hardest part of deduction.  Thank goodness for Anita Harnadek and her Rain and Clouds example.

Wow! On the basis of our first guess, we can eliminate BCA as a possible answer, as well as our guess answer, ABC. On to CAB:

Premise #1: If CAB were the correct order then the computer would have said no chaps in the correct order (as ABC and CAB have no chaps in the same spot in the queue).

Premise #2: The computer did not say no chaps are in the correct order (one chap, it said). Conclusion: CAB cannot be the correct order.

Three eliminated with one guess, so far. On to CBA, the sixth and last possible answer:

Premise #1: If CBA were the correct order then the computer would have said one chap is in the correct order (as ABC and CBA have Baker in the same spot).

Premise #2: The computer did say one chap is in the correct order. Conclusion: No conclusion is possible.

Now, on the basis of one guess, ABC, we have eliminated ABC, BCA, and CAB as possible answers, leaving ACB, BAC, and CBA as possible answers. I want you to keep records of your games using the following format:

Guess #1: ABC (1 chap) Guess #2:

Guess #3:

Guess #4:

Results so far (with guess #):

ABC #1

ACB

BAC

BCA #1

CAB #1

CBA

Note that we have kept track of what our first guess was, ABC and which of the six possible orders was eliminated on the basis of that first guess: ABC, BCA, and CAB. Now, for the second guess, we guess one of the not yet eliminated possibilities, as it wastes turns to guess something you know to be impossible. Suppose that we try ACB and the computer tells us that we had no chaps in the correct order. The syllogisms for the three remaining possibilities are as follows:

Premise #1: If ACB were correct then the computer would have said “Well done!” Premise #2: The computer did not say “Well done!” (It said no chaps.) Conclusion: ACB cannot be the correct order.

Premise #1: If BAC were correct then the computer would have said no chaps (as ACB and BAC have no chaps in the same spot).

Premise #2: It did say no chaps.

Conclusion: No conclusion is possible.

Premise #1: If CBA were correct then the computer would have said no chaps as (ACB and CBA have no chaps in the same spot).

Premise #2: It did say no chaps.

Conclusion: No conclusion is possible.

Our game record will look as follows:

Guess #1: ABC (1) Guess #2: ACB (0) Guess #3:

Guess #4:

Results so far (with guess #):

ABC #1 ACB #2 BAC

BCA #1

CAB #1

CBA

So, we can see that we have used two guesses and eliminated four of the six possibilities. The correct queue must be BAC or CBA. Suppose we guess BAC and the computer tells us that we had no chaps in the right order. That would mean that the correct order must be CBA, which should be our fourth and last guess. The game record would look like this:

Guess #1: ABC (1) Guess #2: ACB (0) Guess #3: BAC (0)

Guess #4: CBA (3)

Results so far (with guess #):

ABC #1 ACB #2 BAC #3

BCA #1

CAB #1

CBA #4 (Correct)

Use game record sheets and play the game of Queue3 until you have completed one set of five, all in four guesses or fewer. Then, go on to Queue4 and meet Doyle, a fourth chap. There are 24 possibilities, starting with ABCD and ABDC. Can you list the other 22? Good. Use paper game record sheets and play the game of Queue4 until you have completed one set of five, all in six guesses or fewer. The game record sheet approach will seem like busy work in Queue3, but will be much appreciated in Queue4.

Since Queue3 and Queue4 were written in BASIC, which is no longer available, I looked for, and, happily, found a pretty good substitute (with modifications) in the Android phone app ‘Logic: Code Breaking’.

In this game, go to Settings:

1. Set number of colors to 3.
2. Set number of columns to 3.
3. Set number of rows to 4.
4. Switch unique colors to on.
5. Switch autocheck to on.
6. Switch sequential positioning to on.
7. Set color theme to orange (easier to see).
8. Set labels and colors to on.
9. Set use the following labels to ABC (for Ash, Baker, Carr, of course).
10. Press the back arrow and select new game.
11. Do five of these in a row, in four turns or fewer.
12. For Queue4, change the first three from 3, 3, 4 to 4, 4, 6.
13. Do five of these in a row, in six turns or fewer.

Good luck!

For Apple users, search for a Mastermind game that allows 3 marbles with 3 spaces and 4 marbles with 4 spaces.

Creative Thinking Puzzlers

Here are some puzzles from Dr. Funster’s Creative Thinking Puzzlers: Level C1, John H Doolittle, The Critical Thinking Company, 1995, ISBN 0894558285.  I recommend this book for extra puzzle-solving practice.  If these are tough, drop back to the easier B1 volume.

Codeword clusters

On each line, write the correct word for each codeword. Use your answers to convert each successive word until you are able to solve the mystery word. (If a Z is shown as a B in one word, Z will be shown as B in all coded words.) 

Puzzle 1

1. The polar bear climbed onto the JRKAKSH.
2. He lost the KCKRQJDP by one vote.
3. HSKKP is my favorite color.
4. They have a hunting CDIHK in the mountains.
5. What is your ACDDI type?
6. And the mystery word is ASJPH.

Puzzle 2

1. She plays on a VNOTVNAA team.
2. Bring the GNRRTM and some nails.
3. The fat content is listed on the ANVTA.
4. Don’t waste your VMTNPG.
5. I had a GNRVDMFTM for lunch.
6. And the mystery word is FATNR.

Puzzle 3

1. The RWYGDLWKBH looks like a big lemon.
2. Check the envelope for a return YZZWDTT.
3. The hero DTOYGDZ the villain’s trap.
4. Grampa’s dad is my RWDYH grampa.
5. Did you get lots of RBLHT on your FBWHJZYP?
6. And the mystery word is GWBOD.

Secret word puzzles

Use each list of clue words to find a three-letter solution word. Beside each clue word is the number of letters that word has in common with the solution. Write the solution in the blank beneath the column. (The solution is a real word. It is not a person’s name. It has no repeating letters.) 

Puzzle 1

FUEL (0)

PANT (0)

ACID (1)

DAWN (1)

SLOW (2)

MICE (2) GASP (1)

________

Puzzle 2

REIN (0)

LAMP (0)

ZERO (1)

DEAF (1)

WORD (2)

SICK (2)

LARD (1)

________

Puzzle 3

TUNE (0)

LAMB (0)

FOUR (1)

FOUR (1)

COLT (2)

PRAY (2) FOIL (1)

________

Shape puzzles

Using the clues given, write the name of each person on the line indicating where he or she is seated. In the clues, “opposite” means that you can draw a direct line through the center of the table from one person to another.

Misters Carson, Carrington, Carter, Carstairs, and Carnegie stayed in separate rooms at a small hotel. During the night in question, one of the five murdered one of the others.

1. Carson, Carstairs, and Carnegie had adjacent rooms on the same side of the hall.
2. Carstairs and Carrington had middle rooms.
3. Carter had a corner room.
4. If Carter was next door to Carrington, then Carson was across from the office.
5. If Carnegie was across from the office, then Carstairs murdered Carson.
6. If Carrington didn’t murder Carter, then Carter wasn’t across the hall from Carnegie.

Where was each person’s room and whodunit?

		Office

Line puzzles

Use the clues to solve each puzzle.

Three houses (101, 103, and 105) are located along Elm Street, which runs west (lower numbers) to east (higher numbers). Jubal, Suniko, and Wynona (in no particular order) each live in one of these three houses. Each owns a different pet, snake, canary, or goldfish (in no particular order), and a different kind of bike, mountain, racer, or hybrid (in no particular order).

1. Suniko lives somewhere west of Jubal.
2. The mountain bike is next door to the racer.
3. The racer and the snake do not both reside in the middle house.
4. Wynona and the racer do not both reside at 101 Elm Street.
5. The canary and the goldfish do not reside next door to each other.
6. The hybrid and Suniko do not both live at 101 Elm Street.
7. The goldfish resides somewhere east of the snake.
8. Jubal and the snake do not both reside in the middle.
9. Jubal and the hybrid do not both live at 105 Elm Street.
10. If the canary lives in the middle house, then Jubal lives at 105 Elm Street. Which of these ladies lives in which house and owns which pet and bike?

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

A CLASSIC TEA PARTY, CIRCULAR TABLE PUZZLE

A woman recently hosted a tea party, to which she invited five guests. The names of the six women who sat down at the circular table were Mrs. Ash, Mrs. Baker, Mrs. Carr, Mrs. Doyle, Mrs. Emry, and Mrs. Fink. One of them was deaf, one was very talkative, one was terribly fat, one simply hated Mrs. Doyle, and one had a vitamin deficiency, and one was the hostess.

The person who hated Mrs. Doyle sat directly opposite Mrs. Baker. The deaf one sat opposite Mr. Carr who sat between the one who had a vitamin deficiency and the one who hated Doyle. The fat one sat opposite Mrs. Ash, next to the deaf person and to the left of the one who hated Mrs. Doyle. The person who had a vitamin deficiency sat between Mrs. Carr and the one who sat opposite the person who hated Mrs. Doyle. Mrs. Fink, who was a good friend of everyone, sat next to the fat person and opposite the hostess.

Can you identify each of these lovely ladies?

Creative reasoning

Definitions

According to the model of problem types presented earlier, creative reasoning is called for when the solutions to a problem are not present initially. In these types of problems, solutions must be generated (created) as well as evaluated. Definitions of creativity vary, but generally contain four characteristics:

■           fluency

■           flexibility

■           originality

■           usefulness

Tests of creativity, such as the Torrance Tests of Creative Thinking, are scored for these variables.

Fluency

Tests often count the total number of responses that a person gives to a question, such as “How many uses can you think of for a brick?” (from the Unusual Uses Test). The concept of brainstorming is to generate as many responses as possible and to delay evaluation of each response as it is made. Linus Pauling exemplifies this approach by claiming to have good ideas by having “a lot of ideas and throwing away the bad ones”. Certainly, an overly critical attitude is the worst enemy of good ideas. It may even be the case that the critical thinking movement, with its emphasis on the rules for evaluating ideas once they are presented, could be lowering the overall quality of ideas that are presented. Of course, we must not overlook the importance of strict evaluation of ideas at some point. One would not send a person to the moon without rigid testing of the transportation device. It just seems to me that “the proof of the pudding is in the eating” and that too many potentially valuable ideas die too quickly in the barren fear of criticism and ridicule.

Creativity requires, then, courage. Social pressure, or the fear of ridicule, is very powerful. Today, as in all times, people only want to be noticed in ways that guarantee approval. Historically, atrocities have involved the passive non-intervention of people who were unwilling to risk the social rejection required to object to the proceedings. To be creative, people often adopt the social role of artist/nonconformist. One gives up any hope of becoming prom queen in order to be free to listen to inner voices before outer voices drown them out.

Flexibility

Suppose that, in response to the Unusual Uses question, “How many uses can you think of for a brick?, you list:

1. Remove dead paint from a fence.
2. Scour swimming pool tile.
3. Sharpen a homemade, wooden spear.

In terms of fluency, we indeed have three good responses. But are they really three responses, or just variations on one response? All three responses tell of uses that take advantage of the rough surface of a brick. Compare them with a response that takes advantage of the heavy nature of a brick, say, as a paper weight (a popular, but fairly impractical example). Or, what about using the brick as a missile to break windows during a riot? (Please do not try this trick at home!) These are not only different uses, but different kinds of uses.

Frequently in problem solving, different solutions to problems are really variations of the same solution. For example, during a war, a general might respond to the ineffectiveness of bombing by ordering increased bombing, trying more of the same rather than something completely different. Flexibility, then, refers to solutions that are qualitatively different and is the real key to creative thinking.

In Scott Adams’ Pirate Adventure, students would face a pirate who would not give up a treasure chest. As good Americans, most would type in the command, KILL PIRATE. When the computer responded, THAT DIDN’T WORK, they would type STRANGLE PIRATE or STRIKE PIRATE or would go off seeking weapons with which to mangle the pirate. The trick was to notice that these responses were not very flexible and to ask, “How else can one get something from someone besides using force?” Almost as soon as the question is asked, answers start to flow in terms of bribery and bartering (both quite as American and virtuous solutions). These, of course, turn out to be more successful and the game proceeds.

Becoming aware of yourself as you solve problems and asking questions about what other things are possible are key to improved creative reasoning and, therefore, improved problem solving.

Attitude

The enemies of fluency are fear of looking foolish and loss of gumption. The enemy of flexibility is arrogance and pride. By which I mean a reluctance to give up an idea because “it’s mine”. We gave birth to that idea and dropping it is tantamount to infanticide. Have you ever stuck with an idea long after you knew it was doomed to failure? Like the problem of throwing good money after bad, we invest something of ourselves in our ideas and simply hate to give them up.

Have you ever been in a meeting when people have stuck with an idea that they were attracted to even after a better idea had surfaced? A scientist, of course, is pledged to an objective attitude toward ideas and data. Linus Pauling is noteworthy not only for “having a lot of ideas” but also for the beautifully detached attitude implicit in giving up “the bad ones”. The trick is to get as many of the possible solutions to a problem “out on the table” before committing to any one of them.

Bruce Johnston, in his song, I Write the Songs, argues that the songwriter is like someone who collects wildflowers in a meadow and brings them back for others to appreciate. How much credit should he take for the beauty of the flowers? Johnston seems to say “At most, some”.

The artist and the scientist are appreciators of beauty rather than pure creators of it. I went to a traveling exhibition of Andrew Wyeth paintings years ago in San Francisco, hoping to see a favorite of mine, a painting of a rock with a tree behind it. (I know what you are thinking and it is rude!) Anyway, I entered this large room and along one wall were about twenty versions of the rock and tree painting. Some were in pencil, some in dry brush, some from straight on, some from the side.

A photograph showed that the tree was some distance from the rock and not behind it at all. Wyeth simply had a lot of ideas and threw away the bad ones. Of course, I would like to own any of these wonderful “bad ideas”.

There is some truth in the nine to one ratio of perspiration to inspiration. But be careful that perspiration doesn’t mean the inflexible pursuit of failed ideas.  Despite years of famine, the Russians under Stalin, and later the Chinese under Chairman Mao, continued to apply Lysenko’s theory of genetics because it was politically correct.  “How many deaths will it take till he knows, that too many people have died?” as the saying goes.

Originality and usefulness

Originality refers to the notion of who was the first person to have come up with an idea.

Usefulness refers to the practical application of the idea at this time. Obviously, I think flexibility is the ball game; and, consequently, I have little use for either originality or usefulness. Both Darwin and Wallace came up with essentially the same ideas at essentially the same time, but Darwin gets the glory. Does this reduce in anyway the excellent problem solving that Wallace did? I don’t think so.

Usefulness is even worse. Mendel’s work in genetics was unappreciated until many years after his death and Van Gogh never sold a painting. Someone once said that a weed is a flower with a poor public relations department. The question I keep coming back to is, “Useful to whom?. For example, the back door of my mother’s mobile home porch in Santa Cruz would not close after the 1989 earthquake because the latch and jamb were too far apart. I loosened the jamb and stuck a penny behind it as a shim and it worked fine. Of what use is a penny in this modern day? Sometimes it can be very useful indeed.  As you may have guessed, I consider flexibility to be the most important aspect of creativity, and, indeed, of problem-solving in general.

Flexibility training

The word association test tells you a word and asks you to tell the first word that comes into your mind.  What if you were asked to tell all the words that come to mind, not just one? How many would you come up with?  Stop now and write down all the associations you can think of to the word “fish” (like “fin”) in the space provided below:

You probably had words like fin, swim, tuna, scales, net, hook, tail, gold, and cat.

Aside

When most people problem-solve, they only generate solutions until they think they have one that will work for them, e.g. “Invade and crush all opposition”. Then they execute that solution and see how it works. Interestingly enough, the next solution they might have generated might have been much superior. The trick to knowing which solution is best is one of attitude. Is the problem at hand something you want to dispense with as soon as possible, or is it an opportunity to make things a little better? Try to develop enough of a detached attitude toward problems to slow yourself down enough that you are willing to stay with the solution-generation phase until a variety of potential solutions have been generated. Then, pick the best one from the batch.

Now, getting back to your list of associations or relatives to the word “fish”, using the following form, attempt to generate sub-lists consisting of the categories into which your responses fall. First, name the category, e.g. parts of a fish and then place your responses on the category sub-list as follows:

A. Parts of a fish	B. Kinds of fish	C. Fishing stuff
1. Fin	1. Tuna	1. Hook
2.	2.	2.
3.	3.	3.
4.	4.	4.
5.	5.	5.
6.	6.	6.
7.	7.	7.
8.	8.	8.
9.	9.	9.

D. Words combined with fish to make a new word	E.	F.
1. Gold	1.	1.
2. Cat	2.	2.
3.	3.	3.
4.	4.	4.
5.	5.	5.
6.	6.	6.
7.	7.	7.
8.	8.	8.
9.	9.	9.

G.	H.	I.
1.	1.	1.
2.	2.	2.
3.	3.	3.
4.	4.	4.
5.	5.	5.
6.	6.	6.
7.	7.	7.
8.	8.	8.
9.	9.	9.

Hopefully, an interesting thing happened to you. As you were adding the items to your categorized sub-lists, you thought of additional items to add to the list. And hopefully, as you looked at the categories you had generated, you were able to think of an additional category or two. This added a whole new dimension to the category “fish.” What this exercise does is to attempt to get you to examine your own thinking (by writing it down) and become aware of additional possibilities that didn’t occur to you before. The importance of this cannot be overemphasized.

Now, go back and fill in the table with as many items and categories as you can think of. You may need more than nine items per category and more than nine categories. Use the facing page for additional items. Of course, in some limited categories, such as, “things that fish do”, you may only be able to think of a few items.

My Crazy Relatives

---

---

---

Creative search

This category of problems encompasses the real world, in which you integrate the skills learned in the other problem categories. Years ago, I played a computer game in the interactive fiction  or text adventure game genre called the Pirate Adventure by Scott Adams. I loved the way this type of game set up an imaginary and fun world of problems to be solved and decided to use the Pirate Adventure in my problem-solving class.  When this adventure was no longer available, I decided to write my own.  These adventures, while published and used in schools, are no longer available, in part because they utilized out-of-date technology.  To guide you to my latest suggestions for text adventures for you to start with, please consult my web page @ https://drdooriddle.itch.io/.  If the text adventure is too difficult to start with, you may find yourself losing gumption rapidly.  Start with an easy one to get your bearings.  After that, you should be fine.  Good luck!

++++++++++++++++++++++++++ WELL DONE!  YOU MADE IT!

THE END

++++++++++++++++++++++++++

APPENDIX 1

Most Recent Article

Using Riddles and Interactive Computer Games to Teach Problem-Solving Skills

John H. Doolittle

California State University, Sacramento

Reprinted from: TEACHING OF PSYCHOLOGY, Vol. 22, No. 1, February, 1995, 33-36.

Cognitive flexibility, which is defined as the ability to generate several categories of possible solutions is identified as the most critical aspect of creativity training. Word tables, interactive computer games, and riddles are used to develop cognitive flexibility. Preliminary results from analyses with quasi-experimental designs provide promising evidence that these methods are effective in enhancing creative and other forms of critical thought in college students.

Ruggiero (1984) took the approach, popular among psychologists, of characterizing the problem-solving process as having two complementary phases: production and judgment. In the production phase, which he associated with creative thinking, potential solutions to the problem are generated. In the judgment phase, which he associated with critical thinking, the ideas generated are evaluated. This approach seems to elevate the importance of teaching students how to generate ideas to a level approaching the importance of being able to evaluate ideas. However, a closer examination of the evaluation process shows that it, too, frequently calls on the problem solver to think creatively (J. H. Doolittle, 1992b). For example, if one is evaluating the assertion, “He must be the killer; he’s holding the murder weapon!,” part of what one needs to do is to generate ways in which someone could be holding a murder weapon and not be the killer. This process includes generating various scenarios or models (Johnson-Laird, 1983), which may or may not involve images, and then judging their plausibility (Kaufmann, 1980).

The purpose of this article is to suggest exercises and activities to help students become better idea generators using riddles and computer games as the context in which problem solving occurs.

Flexibility and Metacognition

Flexibility, which is the process of generating a variety of types of potential solutions, may be more important to good problem solving than fluency, which is the process of generating more potential solutions regardless of type. For students to become more flexible as solutions generators, they need to be made aware of the types of solutions that they are generating. This process, one aspect of self-monitoring or metacognition, is at the heart of successful problem solving and can be improved in the important area of verbal associations by having students construct word tables. In constructing word tables, students brainstorm as many associations as they can think of to a word such as fish. The generation of associations should take approximately 2 min. Next, have them categorize the associations they generated. Each student will produce a word table with categories, such as kinds of fish (guppy,

trout, etc.), parts of a fish (fin, gills, etc.), things you take fishing, and so on. An interesting phenomenon then occurs: Students not only begin to add new associations, such as salmon and scales, to the table but also begin to add new categories, such as places where fish live. J. H. Doolittle and Bourg (1991) showed that brief training with generating associations to one word was followed by increased production on an unrelated, follow-up word. More recently, I assigned 10 word tables as a supplemental homework exercise for those of my students who scored in the lowest 20% of the class on a verbal-association measure. On a later and more difficult verbal-association quiz, 80% (12 of 15) of these remedial students passed the test as compared with 53% (32 of 60) of the other students, who were not required to produce word tables. It may be that any activity that causes problem solvers to pause, retrieve relevant information from memory, and examine their production is beneficial. Flexibility and Mental Models

The notion of thinking as the construction and manipulation of mental models (Johnson-Laird, 1983) suggests another realm for flexibility training. Riddles, puns, jokes, and other word-association games help students shift mental models. The primary skill learned in these exercises is a willingness to let go of an unsuccessful solution or model. It provides a way to circumvent the common problem of functional fixedness in which problem solvers are not able to go beyond the usual functions of an object. Jokes and riddles work because the listener develops a likely model or interpretation, which then proves to be incorrect. For example, in the joke, “Question: How do porcupines make love? Answer: Very carefully!,” the question leads to a distant and clinical mental model of the mechanics of mating, which the answer switches to a porcupine’s perspective of the dangers of being close. The popularity of jokes, puns, and riddles suggest that people enjoy the surprise of shifting mental models in certain situations. This built-in source of motivation can be tapped by the instructor to make the learning of thinking skills fun.

The enjoyment of riddles, as opposed to jokes and puns, calls on the listener to at least attempt to shift the model. In the riddle, “What’s black and white and read all over?” (answer: a newspaper), which works better as a spoken riddle, the solver is fooled by the words black and white to misinterpret read as red. Psycholinguists call these garden path sentences because the reader is misled “down the garden path” by key words in the sentence that suggest another meaning than the one that is intended. To use riddles as a teaching tool, I decided to generate riddles in a sequence from easy to difficult so that solvers would have a reasonable chance of solving each riddle while building their skill level (J. H. Doolittle, 1991). An example of a college-level riddle is as follows:

“What you did to the letter,

Before it was sent;

You memorized the poem,

Not knowing what it meant.” (wrote/rote)

Riddles like this from the Dr. DooRiddles series or other riddles can be selected for appropriate difficulty level and read aloud to the class or presented on an overhead transparency. In these exercises, students must be cautioned against blurting out answers so that others will have a period of quiet in which to generate models and possible word tables. Popular parlor games, such as 20 Questions and Charades, foster model flexibility as well. Because these group settings can inhibit the production of some students, computer riddle exercises have been developed (J. H. Doolittle & T. A. Doolittle, 1992a, 1992b) to allow individuals to solve riddles without social judgment and without getting completely stuck.

Visualization and Imagination

A process similar to the use of jokes and riddles to encourage cognitive flexibility occurs when we read or listen to a story. Symbols and sounds are converted into visual images, models, and scenarios that we continuously transform and examine, in order to comprehend the text. Because readers and listeners have to construct their own mental models, these experiences have been shown to be beneficial to the development of students’ imaginations when compared to comprehension based on film presentations (Greenfield & Beagles-Roos, 1988). Presumably, television and other visual media provide images and models so that the production of mental models and creative imagination on the mart of the recipient are less necessary. In interactive-fictions experiences, such as those available as computer software, one is a participant in rather than a recipient of the story. Although participants make maps and other notations as they move about an imaginary world, it is their mental representation of that world that allows them to speculate about the possibilities of a given scene. For example, in the all-text computer program, “Cursed Castle” (J. H. Doolittle, 1992a), the student must see the dirt floor of the dungeon as a potential hiding place in addition to its more usual use.

Students solving interactive-fiction problems on a computer generate a variety of solutions, but they become frustrated on finding that not one of their solutions leads to progress toward the goal. This frustration can quickly build into discouragement and a sense of failure and must be countered by either the sequencing of task difficulty or the judicious application of hints. For example, in “Hangtown” (J. H. Doolittle, 1989b), students must frighten off a vicious dog barring the entrance to the miner’s shack by threatening the dog with the carcass of a huge rattlesnake. Because most students do not think of this right away, the software monitors each student’s progress and introduces a hint after a judicious amount of floundering has occurred. In this case, the next time the student is in the vicinity of the dead rattlesnake, the student is informed that a coyote has strolled by, seen the dead snake, and run off in terror. If this hint does not work, the student is later given a more direct hint. To determine when and where hints are necessary, the software can record which obstacles are the hardest to overcome and where students seem to get stuck. The instructor can then retrieve this information and improve the flow of the program.

Empirical Evidence for the Effectiveness of Using Riddles and Computer

Games for Training Students to be Problem Solvers

During the past 8 years, I have gathered preliminary data using a quasi-experimental design. The comparison group was several sections of my introductory psychology classes at California State University, Sacramento. Two experimental groups received practice with the riddles and computer games described earlier — students in my freshman-level critical-thinking course and students enrolled in the Summer Academic Study Program (SASP) at the University of California School of Medicine,

Davis. Several dependent measures were used: Cornell Critical Thinking Test (Level X;

Ennis & Millman, 1985), the Ennis-Weir Critical Thinking Essay Test (Ennis & Weir,

1985), the Remote Associates Test of creativity (Mednick & Mednick, 1967), the

Creative Reasoning Test (J. H. Doolittle, 1989a), the Unusual Uses Test of creativity (Guilford, Merrifield, & Wilson, 1958), the Purdue Non-language Test of intelligence (Tiftin, Gruber, & Inaba, 1957), and the Coopersmith Inventory of self-esteem (Coopersmith, 1981). Although the introductory psychology students did not show gains on these measures beyond chance expectation, students in the critical-thinking courses and the SASP students showed statistically significant gains on all of these measures (most at a p<.01). Many of these differential gains have been replicated in five or more different semesters.

Independent analyses conducted by the Dean’s Office at the University of California Medical School, Davis, have indicated an improvement for SASP students in grade point average, undergraduate dropout rates, and medical school admission and retention rates.

Although these results are highly encouraging, they must be viewed as preliminary because of the quasi-experimental design used, the fact that there were some year-to-year changes in the type of test used to assess critical thinking, and the fact that these analyses do not indicate the relative benefits of the various educational experiences of these students.

Conclusions

The principle barriers to a society of better problem solvers may simply be that too few teachers are attempting to teach students the skills of creativity. As teachers plunge into these waters, it may be useful if they follow these few precepts: (a) make cognitive flexibility the top priority; (b) if flexibility is not forthcoming, focus on metacognition; (c) provide tasks that are rich in imagery; and (d) closely monitor the frustration level of students so that the tasks will be fun.

References

Coopersmith, S. (1981). Coopersmith Inventory. Palo Alto, CA: Consulting Psycholgists Press.

Doolittle, J.H. (1989a). The Creative Reasoning Test. Pacific Grove, CA: Critical Thinking Press & Software.

Doolittle, J.H. (1989b). The hangtown trilogy. Pacific Grove, CA: Critical Thinking

Press & Software. Doolittle, J.H. (1991). Dr. DooRiddles. Pacific Grove, CA: Critical

Thinking Press & Software.   Doolittle, J.H. (1992a). Adventures in Danger. Pacific Grove, CA: Critical Thinking Press & Software. Doolittle, J.H. (1992b). Imagining possibilities: A neglected aspect of critical thinking training.   Paper  presented at the International Conference on Critical Thinking and Educational Reform, Rohnert Park, CA.                                                                                                                                       

Doolittle, J.H. & Bourg, T.M. (1991, April). The effects of metacognitive training on a word-association task.  Paper presented at the meeting of the Western Psychological Association, San Francisco.  

Doolittle, J.H. & Doolittle, T.A. (1992a). Escape from the pyramid of riddles. Pacific Grove, CA: Critical Thinking Press & Software.                                           Doolittle, J.H. & Doolittle, T.A. (1992b). The riddle mysteries. Pacific Grove, CA:

Critical Thinking Press & Software.                                                                                                             

Ennis, R.H. & Millman, J. (1985). Cornell Critical Thinking Test (Level X). Pacific Grove, CA: Critical Thinking Press & Software.                                                                                                      

Ennis, R.H. & Weir, E. (1985). Ennis-Weir Critical Thinking Essay Test.   Pacific Grove,

CA: Critical Thinking Press & Software.                                                                                                  

Greenfield, P. & Beagles-Roos, J. (1988) Radio versus television: Their cognitive impact on children of different socioeconomic and ethnic groups. Journal of Communication. 38, 71-91.                         

Guilford, J.P., Merrifield, P.R. & Wilson, R.C. (1958) Unusual Uses Test. Orange, CA:Sheridan Psychological Services.                                            

Johnson-Laird, P.N. (1983). Mental models: Toward a cognitive science of language, influence, and consciousness.  Cambridge, MA:Harvard University Press.                                         

Kaufmann, G. (1980) Imagery, Language, and Cognition.  New York:Columbia

University Press.     Mednick, S.A. & Mednick, M.T. (1967). Remote Associates Test. Boston:Houghton Mifflin.           

Ruggiero, V.R. (1984). The Art of Thinking. New York:Harper & Row.

APPENDIX 2:  

ANSWER KEY

DEDUCTIVE REASONING PUZZLES:

PUZZLE 1:  A=M, B=V, C=W

PUZZLE 2:  A=M, B=V, C=W

PUZZLE 3:  A=W, B=V, C=M

PUZZLE 4:  A=V, B=M, C=W

PUZZLE 5:  A=M, B=V, C=W

OR THESE A:  A=W, B=V, C=M

OR THESE B:  A=W, B=M, C=V

OR THESE C:  A=V, B=M, C=W

OR THESE D:  A=M, B=W, C=V

OR THESE E: A=V, B=M, C=W

OR THESE F:  A=W, B=V, C=M

WHO THE FREG:  A=S, B=F, C=G, D=K, E=Q, F=I

THE ROCKSTARS:  A=WD, B=CW, C=LE, D=FD, E=AP, F=DN

THE TEA PARTY: CLOCKWISE: A=VIT DEF, C=HOSTESS, E=HATE DOYLE, D=FAT, F=DEAF, B= TALKATIVE